从数学上讲,一个复杂的数字是实际数字和虚构数字的组合。相量在复数平面中由一个复杂数表示。
这个复杂的数字表示给出了正弦波的幅度和相位,我们可以通过它分析电路的特性。正弦波形是时间的函数,在时域表示。
通常,相类变换方法用于求解与波形相关的方程,这些方程将时间t的函数转换为radian频率w的函数。
频域方程是代数方程,与偏微分方程的时域方程相比,它更易于求解。
因此,复杂数表示有助于易于求解未知拟补体的代数方程。让我们讨论复数及其操纵技术。
复杂数字
假想数是负实数的平方根。假想的数字由假想单元或J运算符组成,这是√-1的符号。该J运算符用于简化虚构数字。考虑可以简化为√-1×√4=J√4= J2的√-4。
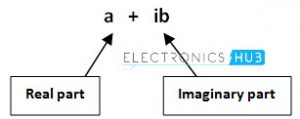
对复数的操作比实数更为复杂,这就是为什么这些被称为复数的原因。一个复杂的数字由两个部分组成,即真实的部分和虚构部分,这些部分由加号或负符号连接,如下所示。
例子:
复杂数字的虚构部分称为“虚构数字”。我们用英语字母“ i”(较低的案例)或j表示。我们将其称为“ i-Ocerator”。一个I操作员被放置在虚构数字之前,以表示虚构部分。例如:i3,i432,i6等。
复数以2维笛卡尔平面表示。这也称为“ S平面”。轴称为“水平轴”和“垂直轴”。垂直轴也称为“真实轴”,并用Y表示。它表示正弦波的幅度或电压范围。
同样,水平轴称为“假想轴”。它用X表示。它表示正弦波的时间段和相位差。在图形方法中,我们将复杂数的真实和虚轴表示为re(z)和im(z),其中z是矩形形式中的复杂数,z = a + ib。
在这里,复杂数字的实际部分也称为“活跃部分”,虚构部分称为“反应部分”。
复杂数字的数学操作规则
- 对于添加和减法:除了假想数字的减法和减法操作,我们将一般数学规则用作实数,即添加或减去两个假想数字时,我们得到了另一个虚构数字。例如:i9 + i5 = i14。
- 用于乘法:虚构数字的乘法遵循不同的规则。也就是说,如果任何两个想象成倍增加,我们将获得一个实际数字。例如:i2 * i3 = 6。
注意:我们还可以通过使虚构部分的系数为“ 0”来将实际数字写为复杂数字。
例如:6可以以复杂的数字为6 + i0。
i-运算符的向量旋转
通常,电压和电流及其相位关系由电向矢量表示,其中矢量的长度代表该数量的大小涉及的,而相对于参考轴的方向代表了电压和电流的正值最大值之间的时间段。
为了根据其X和Y组件指定这些向量,我使用i运算符来区分X轴和Y轴投影。
这是因为y轴投影为+900从X轴投影。这个我的操作员在不改变其大小的情况下旋转矢量。因此,当将 +i运算符作为向量的乘法因子应用时,它会产生900逆时针旋转和-i操作员生产900将其应用于乘法因子的任何向量的顺时针旋转。
将 +i操作员连续乘法向量将产生连续的900向量沿逆时针方向旋转的步骤,而不会影响该向量的大小。
同样,-i操作员连续乘以向量将产生连续的900如下所示,沿顺时针方向旋转的步骤。
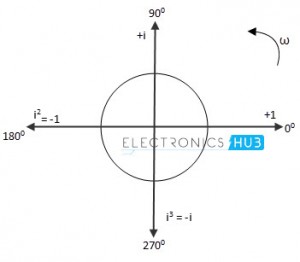
i1 =√-1 = +i»旋转向量900(顺时针逆时针)
i2 = i * i =(√1)2 = -1»旋转向量1800(顺时针逆时针)
i3 = i2 * i =(√1)3 = -i»旋转向量2700(顺时针逆时针)
i4 = i3 * i =(√-1)4 = +1»旋转向量3600(顺时针逆时针)
同样,顺时针旋转表示为
-i1 =-√ -1 = -i»旋转向量-900(顺时针)
-i2 = -1»旋转向量-1800(顺时针)
- (i)3 =√ -1»旋转向量-2700(顺时针)
- (i)4 = 1»旋转向量-3600(顺时针)
复杂数字表示
通常,复数由两种方法表示,它们是
- 笛卡尔或矩形形式
- 使用S-平面
使用矩形形式的复数
如前所述,一个复杂的数字表示为矩形形式的z = a + ib。
在哪里,z是复杂的数字
a是向量的真实部分
b是矢量的虚构部分
我是虚构部分的系数。它的值为√-1。
例如:如果z = 2 + i3,则“ 2”代表真实部分,而“ 3”代表虚构部分。
使用复合或S平面的复合数
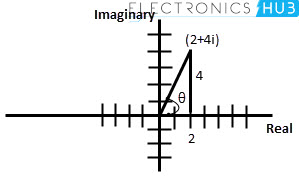
在S-平面表示法中,一个复数表示为笛卡尔平面或S-平面中的点。例如,考虑z = 2 + 4i,其中2是真实的部分,4是虚构的部分。如下所示,它在S-平面中表示。
在这里,复数(2)的实际部分由从正面水平轴上的原点绘制的2个单元表示。假想部分(4i)由从正垂直轴上的原点延长的4个单位表示。
因此,始终假定假想值沿y轴或垂直轴绘制,以及沿X轴或水平轴绘制的真实值。
四个象限编量图
如果将一个实际数字乘以-1,则会将点从原点的一侧移动到另一侧。假设如果+2乘以-1或J2,则新位置等于旋转1800从旧位置。
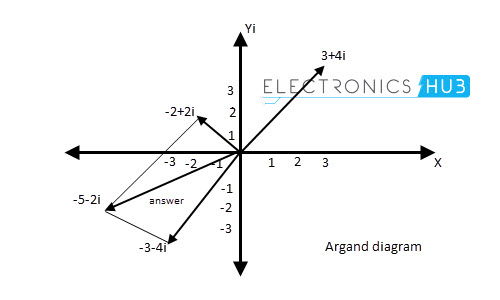
将用j作为矢量旋转乘以的概念是在交替电流电路中使用复数的基础。这个概念导致一个称为Argand图的图,该图表示复数。
在Aragand图中,复数的实际部分表示在X轴上,即RE(Z)。复数的假想部分表示在Y轴上,即IM(Z)。在笛卡尔平面中,复数被定义为(a,b)。
在Argand图上,水平轴代表垂直假想轴右侧的所有正实数和垂直虚轴左侧的所有负实数。假想数表示在原点上方,负虚数的数字表示在垂直轴上的原点下方。
以相同的方式,所有正实数在原点的右侧表示,所有负实数在原点的左侧,水平轴上表示。因此形成了一个具有4个坐标的复杂平面。
Argand图用于表示矢量长度等于复数数量的大小的相旋转。它每2π/ω秒完成一个完整的周期。
00=±3600= + 1 = 1∂00= 1 + i0
+ 900= +√-1 = + i =1蕾 + 900= 0 + i1
- 900= - √-1 = - i = 1∂-900= 0 - I1
±1800=(√-1)2 = - 1 = 1±1800= - 1 + I0
零实际部分的复杂数称为“纯虚构数字”。例如:z = 0 + i2。
具有零假想零件的复杂数字称为“纯实际数字”。例如:z = 2 + i0。
角度和象限
00到900→第一个象限(i)。
900到1800→第二象限(ii)。
1800到2700→第三象限(III)。
2700到3600→第四象限(IV)。
我们可以使用
tan-1(假想组件÷真实组件)
下面给出了所有4个象限中复数的绘制草图。
|
|
|
|
|
|---|---|---|---|
| 1 | 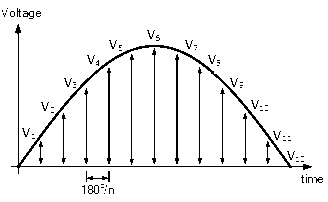
|
A是积极的 b是积极的 论点是积极的 |
Ø=棕褐色-1[B/A] |
| 2 | 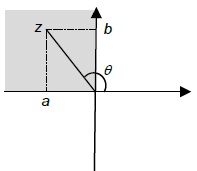
|
A是负的 b是积极的 论点是积极的 |
Ø=π+棕褐色-1[B/A] |
| 3 | 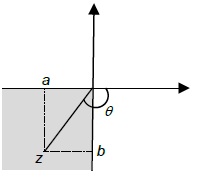
|
A是负的 B是负的 论点是负面的 |
Ø=-π+棕褐色-1[B/A] |
| 4 | 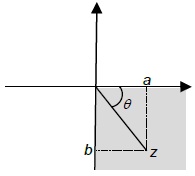
|
A是积极的 b是积极的 论点是负面的 |
Ø=棕褐色-1[B/A] |
复数的加法和减法
如果需要在复数上执行数学操作(例如加法或减法),则首先必须将复杂数将其分为实际部分和虚构部分。
要添加两个复数,请添加真实零件并添加假想的零件。
如果第一个复数数为p = a + ib,第二个复数数为q = x + iy,则给出两个复数的总和
p + q =(a + x) + i(b + y)
p + q =(a - x) + i(b - y)
同样,要减去两个复数,我们减去实际零件并减去虚构部分。
两个复数的差异被给予
p + q =(a - x) + i(b - y)
例子
找到给定两个复数的总和和差异。a = 2 + i4和b = 4 + i3。
添加
p + q =(2 + i4) +(4 + i3)
=(2 + 4) + i(4 + 3)
= 6 + i7
减法
p + q =(2 + i4) - (4 + i3)
=(2 - 4) + i(4 - 3)
= -2 + i1
图形添加和减法
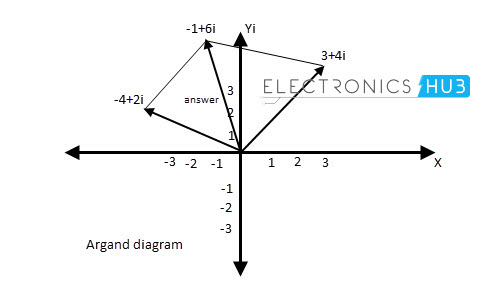
添加复数的方法与使用矢量平行四边形的两个向量相同。下图说明了使用图形方法的3 + 4i和-4 + 2i复数的添加方法。
图中说明了图形方法中(-2 + 2i)的(3 + 4i)的减法。
复数的乘法和划分
复数以与二项式相同的方式乘以乘以,并记住J2 = -1。
考虑两个复数(a+bi)和(c+di),然后给出其乘法
(a+bi)x(c+di)= a(c+di)+bi(c+di)
= AC + ADI + BCI + BD I2
= AC + ADI + BCI + BD(-1)
= AC + ADI + BCI - BD
=(AC - BD) +(AD I + BC I)
=(AC -BD) +(AD + BC)i
假设如果两个复数是(2 + 3i)和(4 + 5i),则其乘法为
(2 + 3i)x(4 + 5i)= 2(4 + 5i) + 3i(4 + 5i)
= 8 + 10i + 12i + 15i2
= 8 + 22i + 15(-1)
= 8 + 22i -15
= -7 + 22 i
分配
复数以与二项式在分母中的自由基分配的方式相同。它涉及找到分母的缀合物。
让我们看看一个复杂数字的示例。
例子
(4 + 2i)÷(3 - i)
((4 + 2i))/((3 - i))=((4 + 2i))/((3 - i))×((3+ i))/((3+ i))
=(12+4i+6i+2i2)/(9+3i-3i-i2)
=(12+10i+2(-1))/(9 - ( - 1))
=(10+10i)/10
=(1+i)/1
= 1 + i
因此,(4 + 2i)÷(3 - i)= 1 + i。
复杂的共轭
复杂数的复杂偶联物是相同的数字,除了虚构部分的符号被更改。通过逆转假想数的符号获得的复数数。
在找到共轭时,实际部分的迹象变得不变。共轭复数由符号z*表示。
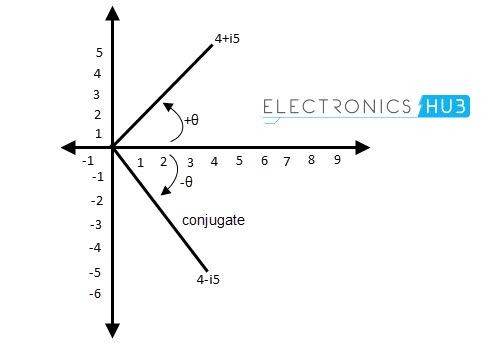
例如,z = 4 + i5的复合偶联物是z* = 4 - i5
复数及其偶联物将具有相同的幅度,并且在X轴上具有相同的水平位置,但是它们的垂直位置在Argand图中完全相反。
关于共轭的事情
- 复杂数及其共轭的总和始终是一个实数(活动组件)。
(4 + i5) +(4 - i5)= 8(一个实数) - 复杂数及其偶联物的减法始终是一个假想的数字(反应性分量)。
(4 + i5) - (4 - i5)= 10i(虚构数字) - 通常,复杂的共轭数用于以矩形形式找到交替电路的明显功率。
使用极性形式的复数
复数可以以极性和矩形形式表示。如上所述,复杂数的矩形形式由真实和虚构部分组成。在极性形式的情况下,复数以大小和角度表示z表示。
±θ。这是向量的大小,θ是相角。它可能是正面的或负面的。
复数的极性形式表示
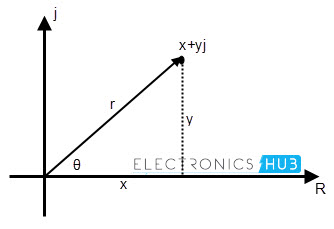
以极性形式表达一个复杂的数字使用三角形和毕达哥拉斯定理的基本三角学概念,以找到用轴形成的幅度和角度。
上图显示了笛卡尔平面中复数X + IY的极性形式表示。这里是由复数数字形成的三角形的结果矢量或对角线。
通过应用毕达哥拉斯定理,我们得到
z2= x2 + y2
z =√(x2 + y2)
矢量成分可以写为x = zcosθ和y = zsinθ。
用真实轴制成的角度给出
θ=棕褐色-1y⁄x
极性形式表示复数的长度和角度。复数及其偶联物具有相同的幅度(模量),它们的角度相反。
例如:复数数字5∂600及其共轭编号5∂-600具有相同的大小。
复杂数字的转换
在分析电子电路的同时,需要将副本从一种形式转换为另一种形式。在矩形形式中,我们分别代表真实轴(水平轴)和虚轴(垂直轴)上复数的真实部分和虚部。
但是在极性形式中,复数简单地表示为童图。现在,让我们了解极性形式和矩形形式的关系和转换,反之亦然。
极性形式向矩形形式的转换(P→R)
极性向矩形形式的转化涉及找到三角水平和垂直成分,以获取X + IY(矩形形式)的真实和虚部。
考虑下面的示例以转换复杂数字4∂30的极性形式0以矩形形式。
矢量成分等于复杂数x + iy的真实部分和虚构部分。所以,
x = acosθ和y = asinθ
令4∂300= x + iy
4∂300=(4cosθ) + i(4sinθ)
=(4 cos 300) + i(4 sin 300)
=(4 x 0.866) + i(4 x 0.5)
= 3.464 + i2
因此,极性形式的复数4∂300等于z = 3.464 + i2。
矩形形式转换为极性形式(R→P)
矩形到极性形式的转换涉及使用毕达哥拉斯的直角三角形定理,该定理由坐标平面中的复合号x + iy与水平和垂直轴形成。
考虑一个示例,将复数数字3.464 + I2的矩形形式转换为极性形式的等效数。
令(3.464 + i2)=
这里a =√(3.462+22)= 3.99(大约4)
θ=棕褐色(-1)2⁄3.46 = 300
因此,矩形形式z = 3.464 + i2中的复数等于4∂300极性形式。
极性形成乘法
执行复数的加法和减法的最简单方法是矩形形式,而极性形式是执行乘法和副本划分的最简单方法。
要执行极性形成的复数的乘法,请首先乘以尺寸,然后添加其角度。
如果z1和z2是(极性形式)中的两个络合物,则为z1 =a1∂θ1和z2 = a2∂θ2。那么这两个数字的乘法将是
Z1 X Z2 =(A1 X A2)∂θ1 +∂θ2
例如:假设两个复数2∂600和5∂450,然后给出其乘法
z1 = 2∂600Z2 = 5∂450
Z1 X Z2 =(A1 X A2)∂θ1 +∂θ2
=(2 x 5)∂600+ 450。
= 10∂1050
极性形式分裂
要执行极地数的划分操作,请首先将两个极点的大小分开,然后减去角度。
(z1) /z2 =(a1 /a2)∂θ1 - ∂θ2
假设两个复数是2∂600和4∂300然后将其划分作为
z1 = 2∂600Z2 = 4∂300
(z1) /z2 =(a1 /a2)∂θ1 - ∂θ2
=(2/4)∂600- 300
= 0.5∂300
使用指数形式的复杂数字
除了矩形形式(a + ib)或极性形式(A诚形式(A诚±θ)表示复数外,还有另一种表示指数形式的复数的方法。
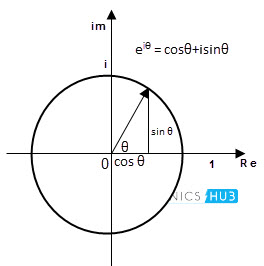
这与极性形式表示相似,涉及通过其大小和相位角度表示复数数字,但具有指数函数e的基础,其中e = 2.718 281。复数的指数形式使用Euler的公式,Eiθ=cosθ + jsinθ。
以指数形式的复杂数的一般表示为
z = a e0iθ
θ在弧度中
该方法表示复数作为笛卡尔平面中的旋转点。该指数形式使用复杂数字x + iy的三角函数或矢量组件(正弦和余弦)。根据Euler的身份,笛卡尔平面中的旋转相图如下所示。
我们可以通过Euler的方法表示任何复杂的数字。Euler的身份使我们能够将复杂数从指数形式转换为极性形式和矩形形式。
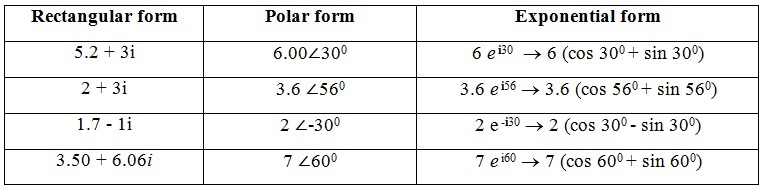
极性,矩形和指数形式之间的关系如下。
z = x + iy =aβ= a(cosθ +isinθ)