布尔代数是一种数学代数形式,用于数字电子的数字逻辑。Albebra由一个语句(通常是数学语句)的符号表示组成。同样,布尔代数中也有表达式、方程和函数。
任何逻辑设计的主要目的都是尽可能地简化逻辑,以便最终实现变得容易。为了简化逻辑,表示逻辑的布尔方程和表达式必须简化。
因此,为了简化布尔方程和表达式,提出了一些定律和定理。使用这些定律和定理,可以很容易地简化或减少任何布尔表达式或函数的逻辑复杂性。
这篇文章展示了一些最常用的定律和定理,布尔代数。
基本法例及证据
布尔代数系统的基本规则和规律被称为“布尔代数定律”。布尔代数的一些基本定律(规则)是
我结合律。
2分配律
3交换律
四、吸收法
诉法律共识
结合律
加法关联定律
声明:
加法的结合律表明,对两个以上的变量进行或运算,即对变量进行数学加法运算,将返回相同的值,而不管在一个方程中变量的分组。
它涉及到分组交换变量。
使用OR运算符的结合律可以写成
+ (B + C) = (A + B) + C
证明:
如果A、B和C是三个变量,那么3个变量每组2个变量的组合将是3种类型,如(A + B)、(B + C)和(C + A)。
根据结合律
(A + B + C) = (A + B) + C = A + B (B + C) = + (C + A)
我们知道,A + AB = A(根据吸收定律)
现在我们假设x = A + (B + C) y = (A + B) + C
根据结合律,我们需要证明x = y。
求Ax = A [A + (B + C)]
= aa + a (b + c)
= A + AB + AC→since AA = A
= (a + ab) + ac
= A + AC→since A + AB = A
= A→since A + AC = A
因此Ax = A
同理,对于Bx = B [A + (B + C)]
= ab + b (b + c)
= ab + bb + BC
= AB + B + BC→因为BB = B
= (b + bc) + ab
= B + AB→因为B + BC = B
= B→since B + AB = B
利用上述方程,我们可以说,A、B、C和+算子之间的关系在乘以其他变量,如x,如xy = yx = x = y时不会发生变化。
yx = ((A + B) + C) x
= (A + B) x + Cx
= (Ax + Bx) + Cx
= (a + b) + c
= (A + (B + C)) y
= Ay + (B + C) y
= Ay + (By + Cy)
a + (b + c)
= x
x = y,也就是A + (B +C) = (A + B) +C = B + (A +C)
例子
取三个变量0,1和0
根据结合律,
(0 + 1) + 0 = 0 + (1 + 0)
1 + 0 = 0 + 1
1 = 1
由此,结合律得到验证。
由此证明了结合律(A + B +C) = (A + B) +C = A + (B +C) = B + (C + A)
关联乘法定律
声明:
乘法结合律是指当变量超过两个时,即对变量进行数学乘法运算,无论在一个方程中变量的分组方式是什么,结果都是相同的。
使用AND运算符的结合律可以写成
A * (b * c) = (A * b) * c
分配律
这是布尔代数中最常用也是最重要的定律,它涉及到两个运算符:与,或。
语句1:
将两个变量相乘,再将结果与一个变量相加,得到的结果与变量与单个变量相乘相加得到的值相同。
换句话说,ANDing两个变量和ORing另一个变量的结果等于and的ORing的变量和两个单独的变量。
分配律可以写成
A + BC = (A + b)(A + c)
这被称为“与”上的“或”分配。
证明:
如果A, B和C是三个变量
A + BC = A*1 + BC→since A*1 = A
= A (1 + B)+ BC→since 1 + B = 1
= a * 1 + ab + BC
= A* (1 + C) + AB + BC→since A*A = A*1 = A
= a *(a + c) + b (a + c)
= (a + c) (a + b)
A + BC = (A + b) (A + c)
由此证明了分配律。
声明2:
两个变量相加,再将结果与一个变量相乘,得到的结果与该变量与单个变量相乘的结果相同。
换句话说,ORing两个变量和andding与另一个变量的结果等于OR的andding的变量与两个单独的变量。
分配律可以写成
A (b + c) = (A b) + (A c)
这被称为与分配或。
证明:
A (B + C) = A (B*1) + A (C*1)→since 1 * B = B, 1 * C = C
= [(ab)*(a *1)] + [(ac)*(a *1)]
=[(ab) * a] + [(ac) * a]
= (a +1) (ab + ac)
= (AB +AC)→since 1 +A = 1
由此证明了分配律。
例子:
取三个变量0,1和0
根据分配律,
0 (1 + 0) = (0*1) + (0*0)
0 (1) = (0) + (0)
0 = 0
因此,分配律得到了验证。
交换律
声明:
交换律是指布尔方程中操作数顺序的互换不会改变其结果。
- 使用OR运算符→A + B = B + A
- 使用AND运算符→A * B = B * A
该定律在布尔代数中也具有较高的优先级。
例子:
取两个变量1和0
1 + 0 = 0 + 1
1 = 1
同样的,
1 * 0 = 0 * 1
0 = 0
吸收法
吸收定律涉及到对二元运算的连接。
i. A+AB = A
2一个(A + B) =
3+ĀB = A + B
(Ā+B) = AB
第三定律和第四定律也被称为冗余定律。
表述一:A + AB = A
证明:
A + AB = A.1 + AB→since A.1 = A.
=A(1+B)→since 1+B = 1
= .
=一个
表述二:A (A + B) = A
证明:
A (A + b) = A A + A b
= A+AB→since A。一个=
= a (1 + b)
= .
=一个
声明3:A + Āb = A + b
证明:
A+ ĀB = (A+ Ā) (A+B)→自A+BC = (A+B)(A+C)使用分配律
= 1 * (A + B)→since A + Ā = 1
= A + B
表述四:A * (Ā+B) = AB
证明:A * (Ā + B) = A. Ā + AB
= AB→自A Ā = 0
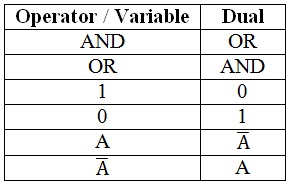
布尔代数中的对偶原理
声明:
对偶原理指出,“表达式的对偶可以通过用ORoperator替换AND,以及替换二进制变量来实现,如用0替换1,用1替换0”。
该定律解释说,替换变量并不会改变布尔函数的值。
但是在交换变量名的同时,我们也必须改变二元操作符。如果一个方程或函数的运算符和变量在方程或函数的输出中不产生变化,尽管它们相互交换,被称为“对偶”。
对偶原理也被称为“德摩根对偶”,它指出“布尔代数中对偶对的互换将得到相同的方程输出”。
对偶性中有一种特殊类型的操作,那就是“自我对偶”。自对偶操作处理输入到输出,不做任何更改。所以这也被称为“不做操作”。
例子:
如果我们有像A + B = 0这样的布尔方程,那么将变量0替换为1,将OR操作符替换为and操作符形成的方程就是A * B = 1。这意味着两个布尔函数都代表了逻辑电路的运行。
根据对偶原理,如果A, B是两个变量,那么在相同的逻辑电路中,方程A + B = 0和A * B = 1都成立。
利用对偶简化布尔函数
利用对偶概念简化布尔函数的实例
(a + b ' c) ' = a ' b c + a ' b c ' + a ' b ' c '
= a ' b (c + c ') + (b + b ') a ' c '
= a ' b + a ' c '–––––––-> (1)
两边取倒数,方程就变成
(a + b ' c) = (a + b ') (a + c)–––––––-> (2)
如果我们观察方程1和2,我们可以观察到与操作符和或操作符是交换的。由此证明了对偶定理。
基于对偶原理,布尔函数可以采用最大项(SOP)和平均项(POS)方法进行简化。
SOP方法的意思是,乘积的和。在这种方法中,布尔变量的最大项被写成它们乘积的和。
POS法的意思是,求和的乘积。在这种方法中,布尔变量的最小项被写成它们和的乘积。
我们将在以后的教程中简要地讨论这些主题。伟德老虎机手机版
德摩根定理
布尔代数涉及二进制数的加法、减法、除法和乘法。与这些基本定律类似,还有另一个布尔代数系统主要依赖的重要定理。这就是德摩根定律。
这也可以被称为德摩根定理。这条法则的作用取决于二元性的概念。对偶性是指将函数中的操作符和变量互换,例如将0替换为1,将1替换为0,将与操作符替换为或操作符,将或操作符替换为与操作符。
德摩根定律就像是对偶原理的延伸。德·摩根提出了两个定理,有助于我们解决数字电子学中的代数问题。
摩根的声明是,
声明1:
“连接的否定就是否定的分离”。或者我们可以把它定义为"两个变量的乘积的互补等于每个变量的互补之和"
(a . b) ' = a ' + b '
声明2:
"分离的否定就是否定的结合"或者我们可以定义为"两个变量和的互补等于每个变量的互补的乘积"
(a + b) ' = a '。B”
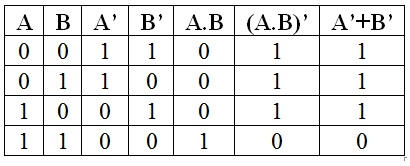
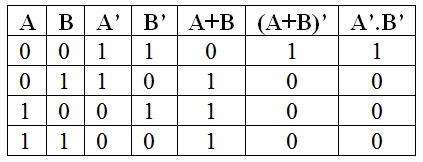
真值表
德摩根定律可以用真值表简单地解释。
德·摩根的第一个陈述((A.B) ' = A ' + B ')的真值表如下所示。
因此,德摩根第一定律也可以表述为“非(A和B)等于(非A)或(非B)”。
德·摩根的第二个陈述((A + B) ' = A ' .B ')的真值表如下。
所以德摩根第一定律也可以表述为" not (A or B) = (not A) and (not B) "
《门》中的摩根定理
德摩根定理可以用与门、或门等基本逻辑门来证明。
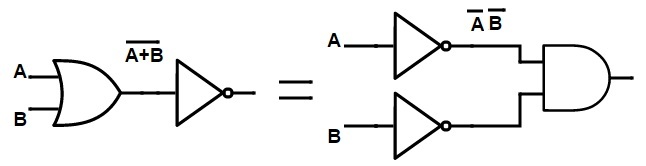
对于语句1:(A.B) ' = A ' + B '
与门(输出端带有非门的与门)的输出等于在OR门的输入端连接两个非门而形成的门的输出。这可以说是,
NANDgate=冒泡或门
对于表述二:(A + B) ' = A '。B”
一个NOR门(或门的输出端有一个非门)的输出等于在AND门的输入端连接两个非门所形成的门的输出。这可以说是,
NOR gate=气泡和gate
让我们看一些例子来理解德摩根定理是如何用来简化布尔方程的。
示例1:
用德摩根定理简化下面的布尔方程。
F =((a . b̅)̅)。(b̅+ c)̅
索尔:
假设F = ((A . b̅)̅)。(b̅+ c)̅
= (((a .b̅)̅)̅+ ((b̅+ c))̅
= (a .b̅)+ (b̅̅.c̅)
= (a .b̅)+ (b.c̅)
因此,方程的简化形式为F = (A .B̅)+ (B.C̅)
示例2
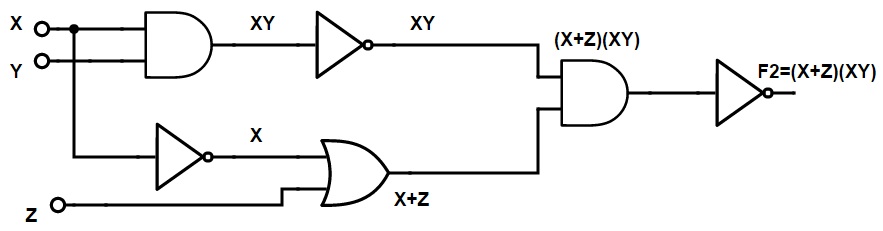
简化设计糟糕的逻辑电路,并为输出方程找到简化的布尔方程。
索尔:
在给定的电路中,输出方程为,
F2= ((a̅+ c).((ab)̅))̅
=((a̅+ c)̅)+ (ab)̅̅
= ((a̅+ c)̅)+ ab
= (a̅̅c̅)+ ab
= (ac̅)+ (ab)
因此,给定电路的简化输出为f2 = (AC̅)+ (AB)。
共识定理
一致定理是布尔代数中的一个重要定理,用于求解和简化布尔函数。
声明
一致性定理指出,当函数中的项彼此互为倒数时(如a和a̅),分离的一致性项被定义。一致定理有两个表述(范式及其对偶)。他们是
Ab + Āc + bc = Ab + Āc
(a + b)(Ā+ c)(b + c) = (a + b)(Ā+ c)
共识定理的证明
表述一:AB+ĀC +BC = AB+ĀC
Ab + Āc + bc = Ab + Āc + bc .1
= AB + ĀC + BC (A + Ā)→since A + Ā = 1
= ab + Āc + ABC + Ābc
= ab (1 + c) + Āc (1 + b)
= AB + ĀC→since 1 + B = 1 + C = 1
例子
利用一致定理证明了A ' bd ' + BCD + ABC ' + AB ' d = BC ' d + AD + A ' BC
索尔:
A ' bd ' + BCD + abc ' + ab ' d = A ' bd ' + BCD + abc ' + ab ' d + A ' bc + bc ' d + abd
= AD + a ' bd ' + BCD + abc ' + a ' bc + bc ' d '
= AD + a ' bc + bc ' '
对偶一致定理
对偶一致定理的表述是
(A + B) (B + C) (' + C) = (A + B) (A + C)
证明
第一步:减少等式左边的量
(A + B) (B + C) (' + C) = ((A + B) (B + C)) (' + C)
=(ab + ac + bb + bc)(a ' + c)
= (ab + ac + b + bc) (a ' + c)
=(ab + ac + (b + bc)) (a ' + c)
= (ab + ac + b) (a ' + c)
= (b + ab + ac) (a ' + c)
= ((b + ab) + ac) (a ' + c)
= (b + ac) (a ' + c)
= a 'b + BC + aa 'c + acc
= a 'b + BC + 0 + ac
= a 'b + BC + ac
第二步:减少等式右边的量
(a + b) (a ' + c) = aa ' + a ' b + ac + BC
=0 + a 'b + ac + BC
= a 'b + ac + BC
现在我们可以看到,R.H.S. = L.H.S.
因此,证明了一致定理的对偶性。
香农定理的扩张
著名的理论家和数学家克劳德·香农在对布尔代数函数的简化进行研究后,提出了一些公式。这就是香农展开定理。这些函数用于扩展关于单个变量的布尔函数。
定理1:
f (A1,A2, A3, . . . .Ai . . . .An) = Ai。f (A1, A2, A3, . . . .1、……A)+ A̅i。(a1, a2, a3, . . . .0,…一个)
例子:
f (A, B, C, D, E, f) = C。f(A, B, 1, D, E, f) + C̅。f (A, B, 0, D, E, f)
定理2:
f (A1, A2, A3, . . . .Ai . . . .a) = [Ai + f (A1, A2, A3, . . . . . . .一个)。[A̅i + (A1, A2, A3, . . . . .1、……一个)
例子:
f (A, B, C, D, E, f) = (C + f (0 A、B、D、E、f)]。[C̅+ f (A, B, D, E, f))
用香农展开定理简化布尔函数
练习1:
用香农展开定理展开给定的布尔函数。
f (A, B, C, D) = A B̅+ (A C + B) D
Sol:给定函数是
f (A, B, C, D) =A B̅+ (A C + B) D
=[1。B̅+ (1;C + b) d] + a̅[0。B̅+ (0;C + b) d
= a [b̅+ (c + b) d] + a̅[b d]
= a b̅+ a (c + b) d + a̅b d
练习2:
用香农展开定理展开给定的布尔函数。
f (A, B, C, D) = A̅C+ (B + AD
索尔:
给定的函数
f (A, B, C, D) = A̅C+ (B + AD
= a[1̅.]C + (b + 1;D) c] + a[0̅。C + (b + 0);D) C)
= 0;C + (b + d) C] + a [1;C + (b + 0);D) C)
= a (b + d) c + a̅(c + bc)
香农的减少定理
利用香农约简定理对单变量布尔函数进行约简。
定理1:
人工智能。f(A1, A2, A3, . . . .Ai . . . ., An) = Ai。f(A1, A2, A3, . . . .1、. . . .一个)
Ai+ f(A1, A2, A3, . . . .Ai . . . ., An) = Ai+ f(A1, A2, A3, . . . .0, . . . .一个)
例子:
B。f (A, B, C, D, E, f) = B。f (A, 1, C, D, E, f)
B + f (A, B, C, D, E, f) = B + f (0 C, D, E, f)
定理2:
(A_i)̅。f(A1, A2, A3, . . . .Ai . . . ., An) = (A_i)̅。f(A1, A2, A3, . . . .0, . . . .一个)
(A_i)̅+ f(A1, A2, A3, . . . .Ai . . . ., An) = (A_i)̅+ f(A1, A2, A3, . . . .1、. . . .一个)
例子:
B̅。f (A, B, C, D, E, f) = B̅。f (A, 0, C, D, E, f)
̅B + f (A, B, C, D, E, f) = B̅+ f (1 C, D, E, f)
用香农约简定理简化布尔函数
练习1:
利用香农约简定理展开给定的布尔函数。
f (A, B, C, D) = A [A̅(B + C) + (A + D)]
Sol:给定函数是
f (A, B, C, D) = A [A̅(B + C) + (A + D)]
=一个。[1 ' (b + c) + (1 + d)]
=一个。[0 (b + c) + (1 + d)]
=广告
练习2:
利用香农约简定理展开给定的布尔函数。
f (A, B, C, D) = A + A ' B + A C ' (B + C) (B + D)
Sol:给定函数是
f (A, B, C, D) = A + A ' B + A C ' (B + C) (B + D)
= a + 0 ' b + 0 ' c ' (b + c) (b + d)
= a + 1。B
= a + b

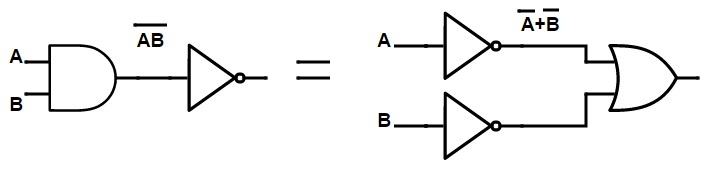
一个回应
回答得好,对学生很有帮助