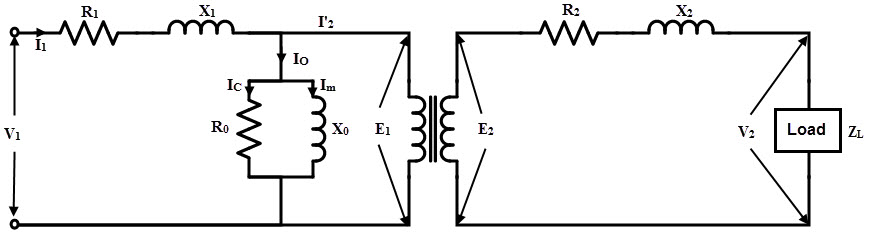
作为静态设备，变压器可以具有高达98至99％的效率范围。理想的变压器绝对与实际变压器不同。由于存在弯曲电阻，漏通量和其他损耗，实际变压器的性能可以偏离理想的变压器。
考虑到所有这些效果，以评估变压器的性能在负载或无负载上。本文将有助于一个了解变压器在负载条件下的表现及其属性以及无负载条件。
大纲
理想的空载变压器
虽然没有一种变压器是理想的，但在其设计的运行过程中，变压器会接近其理想的特性。理想的变压器没有一次绕组和二次绕组的电阻。主要环节与次要环节产生的全部通量，因此没有泄漏通量。
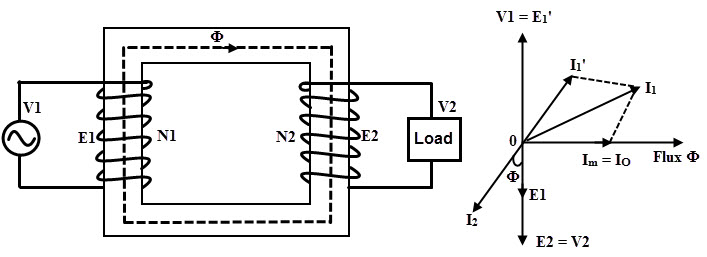
而且，由于芯的无限渗透性，它具有无限量的磁通量而不会饱和。忽略了核心和磁芯的磁滞损失。当该理想的变压器在无负载上操作时，次级电流为零（次级端子是打开的），如下图所示。
当主要用电压V激励主要兴奋剂时1时，主绕组引出电流I1在核心中产生必要的助焊剂。该电流称为磁化电流IM.．随着绕组纯属电感，绕组阻力为零。
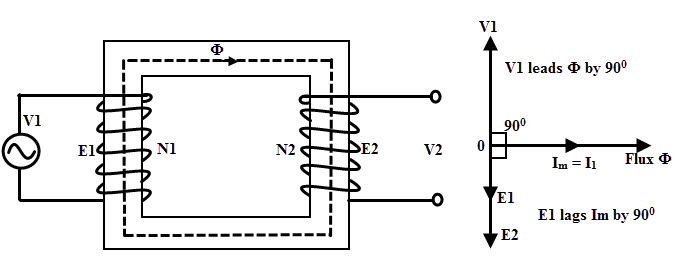
由于这种纯电感，磁化电流iM.滞后电源电压V1通过90度。当前我M.非常小并产生与电流IM.如图所示。
该磁通量与初级和次级绕组都有并产生EMFS E.1和E2在各个绕组中。这些诱导的EMF对电源电压V相反1（这是伦敦法律的局部制作EMFS的原因。因此，E.1与v的幅度相等1但反相1．
同样的是E.2是与V1反相的，但其幅度取决于次相的匝数，即N2．因此，两个电动势都是E1和E2与V1不相，且彼此相，如图所示。变压器的输入功率是一次电压和电流的乘积以及它们之间的余弦角。
这里，主电压和初级电流（或磁化电流）之间的相位角是90度。余弦90为零，因此电源输入为零。这是因为在没有负载下，次级或输出功率为零，也是由于理想的功率，损耗也为零。因此，在没有负载下的理想变压器的输入功率为零。
理想负载变压器
考虑加载理想的变压器，负载的性质是电感，因此输出或次级电流滞后由输出或次级电压V2通过角度φ如图所示。这个二级电流i2产生二次磁通，反对芯中的主通量。所以mmf n2一世2被称为退磁安培转动。
为了减少二次通量对主助焊剂的影响，主要提取额外的电流i1”。这种电流称为电流的负载分量。安匝N1一世1'平衡n2一世2安培转动，以便净通量保持不变。因此我的目前1'与我的方向相反2它的幅度由我决定1'= n2/ N1×I.2．
现在主电流由磁化电流组成，以产生磁通量和电流I的负载分量1”。因此，我1= I.M.+ I.1”。将上述相量与具有理想变压器的相位器与无负载进行比较，主要电流仅在它们之间产生差异。
由于零阻力下降，次级诱导的EMF2等于v2和图中所示的方向相同。
无负载的实用变压器
实际的变压器由于各种原因而与理想的变压器不同，如核心的有限渗透率，在两个绕组等中的有限绕组电阻和泄漏通量等。当核心经受交替的磁通量时，发生涡流和磁滞损耗核心。
这些被称为铁或核心损失。实际变压器的初级绕组具有一定的阻力，因此还存在小的初级铜损失。因此，当实际变压器运行时，需要主要电流来提供核心和绕组损耗。
因此，无负载电流由两个组件组成。第一组分是磁化成分IM，其负责在芯中产生必要的通量。另一个组件是活动或核心损耗分量IC，其提供核心的总损失。所以主要电流
一世O.= I.M.+ I.C
由于实际变压器中的绕组电阻，空载电流Io不再滞后于90度角的电压。因此，Io滞后于电压V1一个角度Φo，因此无负载功率因数存在，如图所示。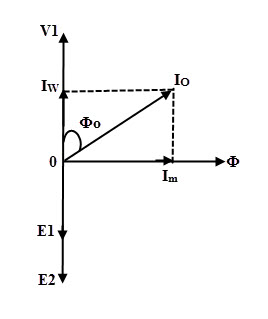
根据上面的相量图，
空载电流的磁化分量，IM.= I.O.罪Φo
空载电流的铁芯损耗分量，IC= I.O.cosφo.
空载电流的大小，IO.=√(我2M.+ I.2C的）
其中φo没有初级电压和电流之间的负载角度。
总电源输入无负载，WO.= V.1×I.O.×cosφo.
应注意，对于设计良好的变压器，初级的载荷电流约为额定或满载电流的3％至5％。由于弯曲性小，铜损损耗可忽略较小。因此，在无负载上操作的实际变压器的电源输入代表变压器中的铁损，并且在所有负载条件下是恒定的。
W.O.= V.1×I.O.×cosφo=铁损失
具有无负载示例的变压器
假设变压器接在400v、50hz的电源上运行，变压器无载电流为5A，滞后功率因数为0.3。为此，我们计算了空载电流的磁化分量和铁损。
从上述数据，φO= COS -1（0.3）
= 72.54度
因此，我M.= I.O.罪Φo
= 5×SIN 72.54
= 0.953 A.
铁损失，p一世= V.1×I.O.×cosφo.
= 400×5×0.3
= 600瓦
负载变压器（无绕组抵抗和漏电抗）
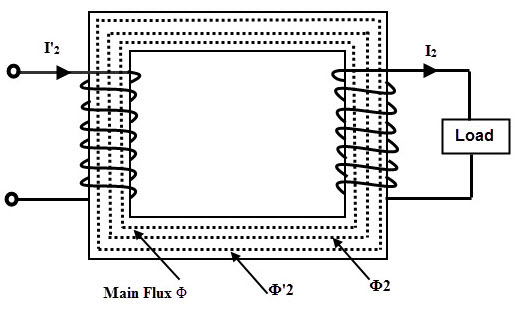
负载连接到变压器时的那一刻，次级电流开始流过负载。取决于在次级连接的负载，二次电流i的幅度和相位2是多种多样的。
在电阻载荷的情况下，我2与v相位2，如果它是归纳我2滞后V.2并且对于电容负载I2引导V.2．由于二级mmf n2一世2，二次电流i2在核心中设置磁通量φ2。
这种次级磁通与由磁化部件产生的主磁通相对。这种磁动势称为消磁安匝。由于磁通量的这种对立，在初级电动势中产生的电动势1减少。
由于增加的向量差v，主要从供应中提取更多电流。1- E.1．这个额外的电流图是由于负载，因此称为初级电流I2 '的负载分量。
该负载分量电流具有I2的抗相位，并产生磁通Φ2'以中和φ2的效果。因此mmf n1一世2'平衡mmf n2一世2．因此，变压器中的净通量是恒定的，变压器也称为恒定的磁通机。
从上面的讨论，
N.1一世2'= n2一世2
一世2'=（n2/ N1）一世2
一世2'= k i2
因此主要电流i1载荷下的变压器有两个组件。第一个没有负载电流IO，其具有磁化组件IM和核心损耗组件IC．
该初级电流通过电源电压滞后于φO的角度。其他电流是当前I的负载分量2’，与二次电流I反相2．该电流的阶段由连接的负载性质决定。
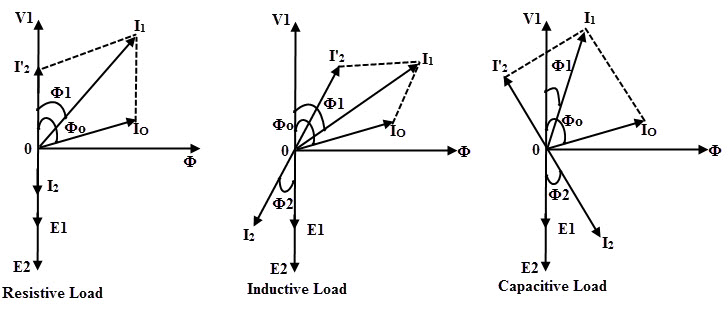
可以注意到，通过忽略实际变压器中的各种液滴如电阻和漏电抗液滴所描述的上述说明。因此，e2与v相同2．以上的三个图显示了用于使用不同负载运行的变压器的相量图。
一次电流I1是我的电流的矢量和O.和我2”。二次电流i2滞后V.2由一个角度Φ2为感性负载。在电阻负载中，I2与e相阶段2在电容负载中，我2引导E.2由角φ2如图所示。
载荷变压器（耐绕组电阻和漏电抗）
实际变压器绕组具有一定的阻力。这些初级和次级绕组的这些电阻不仅导致电压降低1R.1和我2R.2在各自的绕组中，但欧姆损失我12R.1和我22R.2．
当电流流过主要i时1，绕组阻力导致电压降I1R.1因此，在一次电源中感应的电动势不再等于电源电压V1．
所以，E.1= V.1- 一世1R.1
类似地，由于I，在次级中引起的EMF不会出现在负载终端上2R.2在次级绕组下降。
所以，V.2= E.2- 一世2R.2
在上述两个等式中，减法应被向量方式执行。这些滴剂是纯电阻因此，这些都处于相位的电流。
而且，在实际变压器中，除了链接初级和次级绕组的相互或有用的焊剂之外，单独完成通过空气的路径的磁通量的一小部分，单独地称为漏漏通量。
初级泄漏通量由电流I1产生，仅使用初级绕组。并且二次泄漏通量由电流I2产生，仅使用次级绕组。这些泄漏通量导致自诱导的EMFS e2和E2在他们各自的绕组中。
因此，生产e1在主要的情况下，电源电压必须克服主要诱导的EMF。类似地生产辅助端子电压V2，诱导的EMF e2必须克服由漏磁引起的二次自感电动势。
这些EMF被认为是跨越绕组连接的虚拟电抗的电压降或电抗液滴。因此我1X1是主要的反应滴和我2X2是二次电抗降。
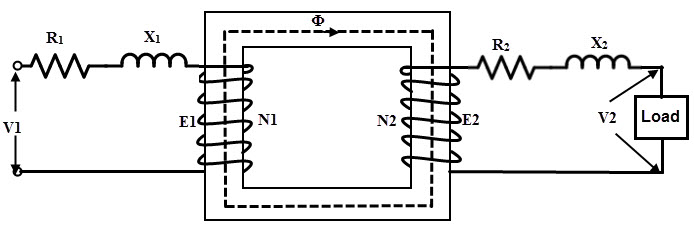
然后，变压器的基本电压方程变为
E.1= V.1- 一世1R.1- 吉1X1
V.2= E.2- 一世2R.2- 吉2X2
因此，通过考虑泄漏电抗和绕组阻力的影响，可以如下图所示的变压器。
此外，变压器中由一次电流携带的无负载电流需要维持铁心中的互感器磁通以及响应铁心损耗。在空载等效条件下，实际有载变压器如下图所示。这也称为变压器的等效电路。
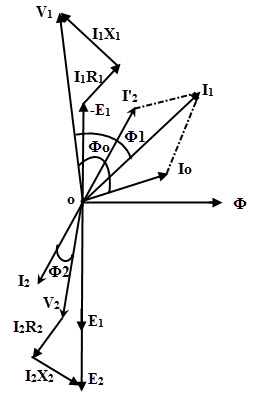
下图显示了具有负载操作的变压器的相位图。二次电流i2滞留在负载v上的电压2通过一个角度Φ2，所以负载的功率因数是cos Φ2。”
下我2R.2在二级侧与二次电流相位，而我2X2参考电流i将引线达到90度2．通过将这些滴剂添加到v2，我们得到诱导的次级EMF e2如图所示。
一世2'当前流入主要电流I对应于二级电流i2．io是没有我的负载电流M.和我C组件。因此，在初级电流中流动的总电流是I的相量和2’和伊俄，如图所示。- e1是感应电动势在初级，这是一个磁通量的头90度。
初级绕组阻力下降1R.1与我相当1泄漏掉落我1X1参考I引导90度1．因此，通过添加-e1和下降我1R.1和我1X1我们得到电压V1，如Phasor图中所示。
